Система упражнений

В данной главе представлены задания, на формирование алгоритмических умений у учеников. Задания разбиты на три раздела, в первом, представлены примеры, в которых основной идеей тождественного преобразования являются формулы сокращенного умножения, во втором, за основу взяты свойства тригонометрических функций, а третий раздел содержит показательные и логарифмические выражения.

Задания составлены, таким образом, что при решении первого пункта, становится виден алгоритм для решения последующих, но при этом задания существенно усложняются.

Формулы сокращенного умножения

1. Представьте в виде произведения:

а) ;

б) ;

в) .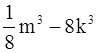

Решение

а);

В пункте а) формула разности кубов береться за основу, с помощью которой формируется алгоритмические умения при решении следующих пунктов:

б) ;

В пункте б) уже ученик раскладывает число 64 как , чтобы следующим шагом было разложение по формуле сумме кубов.

в)

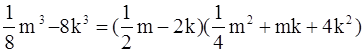
В пункте в) для успешного разложения ученику потребуется представить не только одно из слагаемых, но и второе, причем в сочетании с буквенными выражениями для этого и представим как и соответственно, а дальше все раскладывается по формуле разности кубов.

Как видно данное задание формирует алгоритм разложения выражения используя формулу суммы и разности кубов.

2. Преобразуйте в двучлен:

а) ;

б) ;

в) .

Решение

а) ;

В пункте а) явным образом дана формула разности кубов, это тот алгоритм, который ученик сможет применить, производя тождественные преобразования в последующих пунктах.

б) ;

В пункте б) так же представлена формула разности кубов, ученик применяя алгоритм, сворачивает данное выражение

в) .

В пункте в) осложнение может вызвать коэффициент, стоящий перед , но вспоминая формулу, и применяя алгоритм сворачивания, ученик сделает тождественное преобразование.

3. Представьте в виде произведения:

а) ;

б) .

Решение

а) ;

б) .

4. Выделите полный квадрат:

а) ;

б) ;

в) ;

г).

Решение

а) ;

б) ;