Теоретико-множественный смысл понятия числа и арифметических действий над ними

Рис.6.

б) уменьшение множества, равночисленного данному, на несколько предметов:

Рис.7.

в) сравнение двух предметных множеств, т. е. ответ на вопрос «На сколько предметов в одном множестве больше (меньше), чем в другом?»:

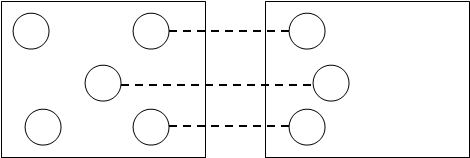
Рис.8.

В процессе выполнения предметных действий у ребенка формируется представление о вычитании как о действие, которое связано с уменьшением количества предметов.

Рассмотрим конкретный пример: «У Маши было пять кукол. Две она подарила Тане. Покажи куклы, которые у нее остались». Дети рисуют 5 кукол, зачеркивают 2 и показывают куклы, которые у нее остались.

Рис.9.

Для разъяснения смысла вычитания, также как и сложения, можно использовать представления детей о соотношение целого и части. В этом случае куклы, которые были у Маши («целое»), состоят из двух частей: «куклы, которые она подарила и куклы, которые у нее остались».

Часть всегда меньше целого, поэтому нахождение части связано с вычитанием. Обозначая части и целое их числовыми значениями, дети получают выражение 5 – 2 или равенство 5 – 2 = 3. В процессе выполнения у детей формируется представление о понятие «меньше на».

Из курса математики нам известно, что если а и в целые неотрицательные числа, то:

а) а · в = а + а + а + … + а, при в < 1;

в слагаемых

б) а · 1 = а, при в = 1

в) а · 0 = 0, при в = 0

Теоретико-множественная трактовка этого определения лежит в основе разъяснения младшим школьникам смысла умножения. Она легко переводится на язык предметных действий и позволяет для усвоения нового понятия активно использовать ранее изученный материал. Для осознания необходимости введения нового действия можно использовать различные реальные ситуации. Например: учащимся предлагается подсчитать количество кафельных плиток, необходимых для выкладки стены на кухне. Стена имеет форму прямоугольника разбитого на квадраты (это может быть клетчатая часть доски). Они, естественно, начинают действовать способом по единичного счета клеток, но скоро обнаруживают трудоемкость такой работы. Подчеркнув это, учитель ставит задачу найти более простой путь поиска ответа. Конечно, сами учащиеся могут не менее при этом будут созданы благоприятные психологические условия для его принятия.